Relación entre el 8 de marzo y los fallecimientos por COVID-19

*Artículo de opinión. — Por Roberto Mínguez Solana.*

Las noticias de los últimos días sobre las actuaciones de nuestro gobierno con respecto a la crisis del COVID-19 no dejan de sorprendernos, incluso las manifestaciones de nuestros supuestos expertos, que son capaces de utilizar de forma simultánea frases como: “Un brote por una pequeña fiesta inocente puede ser el inicio de una nueva epidemia” y “Si ha tenido algún efecto, ha sido marginal”, refiriéndose al posible efecto de las manifestaciones del 8M en el número total de fallecidos. Dado que nos dedicamos al análisis de datos, nos vemos en la obligación moral de tratar de analizar de la forma más rigurosa y objetiva el posible efecto que ha tenido el 8M en el devenir de nuestro país en términos de fallecidos por COVID-19.

Antes de comenzar, vamos a contextualizar nuestro trabajo en el análisis del COVID-19. Llevábamos un tiempo sin actualizar nuestros modelos ni publicar nada y, a día de hoy, estamos en disposición de decir que hemos acertado en todas nuestras previsiones.

Así, por ejemplo:

• El 31 de marzo dijimos en COPE Ciudad Real que estábamos en torno al pico de fallecimientos por COVID-19 diarios, lo cual podemos confirmar con los datos actuales.
• El 8 de abril, confirmábamos en Castilla-La Mancha TVE que las medidas de confinamiento estaban funcionando.
• El jueves 9 de abril lo confirmábamos también en La Tribuna de Ciudad Real.
• El 25 de abril pronosticábamos que en torno a la segunda mitad de mayo llegaríamos al receso en el número de fallecidos, lo cual podemos corroborar estos días.
• También insistimos en que la ventaja del modelo que proponíamos es que, pese a que los datos de fallecidos no fueran precisos, la dinámica temporal de evolución del virus no se veía afectada, y por eso los picos no se han modificado. Obviamente sí que afecta al número total de fallecidos, como parece que está pasando. De hecho, antes hemos publicado un video explicando el método que creemos más apropiado para estimar los fallecidos por COVID-19 usando el sistema oficial MOMO. Es precisamente ese método el que nos ha permitido hacer este último análisis que aquí os presentamos.

Una vez puesto en contexto nuestro trabajo previo…

… El 27 de mayo nos descargamos el fichero disponible del sistema MOMO, tal y como explicamos en el video. No empleamos los datos oficiales porque, y cito textualmente: “DEBIDO A LA ENTRADA EN VIGOR DE LA NUEVA ESTRATEGIA DE VIGILANCIA Y CONTROL EN LA FASE DE TRANSICIÓN DE LA PANDEMIA DE COVID-19, HAY UN CAMBIO EN LA NOTIFICACIÓN DE LAS CCAA AL MINISTERIO DE SANIDAD QUE AFECTA A LA INFORMACIÓN DE ESTE PANEL. LAS SERIES DE CASOS DIARIOS ESTÁN EN REVISIÓN POR LAS CCAA. CUANDO SE CONSOLIDE LA INFORMACIÓN, SE PROCEDERÁ A LA ACTUALIZACIÓN DEL PANEL DE COVID-19”. En cualquier caso, si empleamos los datos del MOMO y nos centramos en el país en su conjunto y en las comunidades más afectadas, las cifras son demoledoras:

1. En España, pasamos de 27892 fallecidos oficiales a día 21 de mayo, a los 42184 que arroja el MOMO. Recordamos que estos son fallecidos que exceden el 99% de las bandas de confianza del MOMO.
2. En Madrid, pasamos de 8912 fallecidos oficiales a día 21 de mayo, a los 13706 que arroja el MOMO.
3. En Cataluña, pasamos de 6021 fallecidos oficiales a día 21 de mayo, a los 10797 que arroja el MOMO.
4. En Castilla-La Mancha pasamos de los 2913 fallecidos oficiales a día 21 de mayo, a los 5126 que arroja el MOMO.
5. En Castilla-León pasamos de los 1960 fallecidos oficiales a día 21 de mayo, a los 3080 que arroja el MOMO

La siguiente pregunta que nos hacemos…

… Especialmente a raíz de las últimas noticias sobre la polémica del posible efecto del 8 de marzo en el balance oficial de víctimas, es: ¿tuvo una influencia significativa las celebraciones del 8 de marzo en ese balance final? Vamos a tratar de dar una respuesta basada única y exclusivamente en lo que dicen los datos y lo que se sabe a día de hoy de la evolución de un paciente infectado con COVID-19.

Como paso previo a nuestro análisis, necesitamos saber cuánto tiempo transcurre desde que una persona se contagia hasta que fallece. Obviamente la respuesta a esta pregunta es una variable aleatoria de la que hemos definido sus características con distintas fuentes:

1. La primera fuente procede de un médico español, el Dr. Iván Moreno, internista del Instituto Médico Ricart IMR que muestra el gráfico siguiente en el que establece que el tiempo que pasa desde que un paciente se contagia hasta que fallece ronda entre 21 y 25 días.

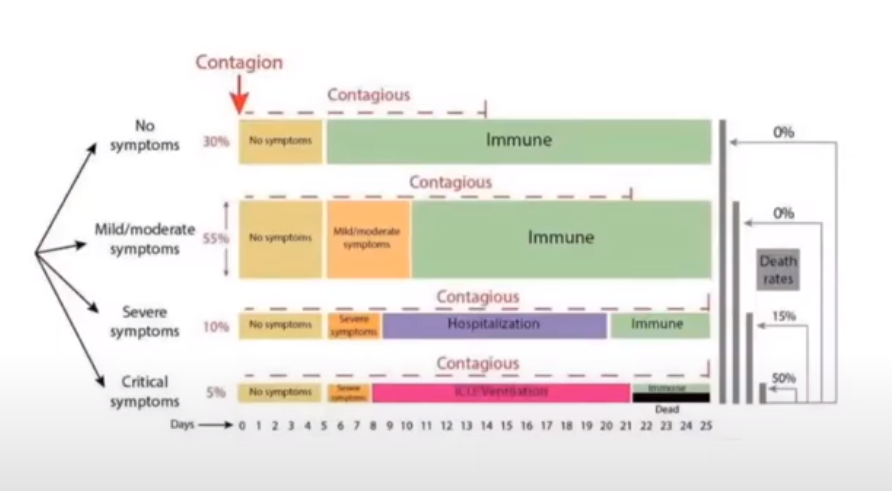
2. En este artículo se presenta información análoga, aunque amplía la ventana temporal desde el contagio hasta el fallecimiento de 2 a 4 semanas, llegando incluso hasta 10 semanas en algunos casos.

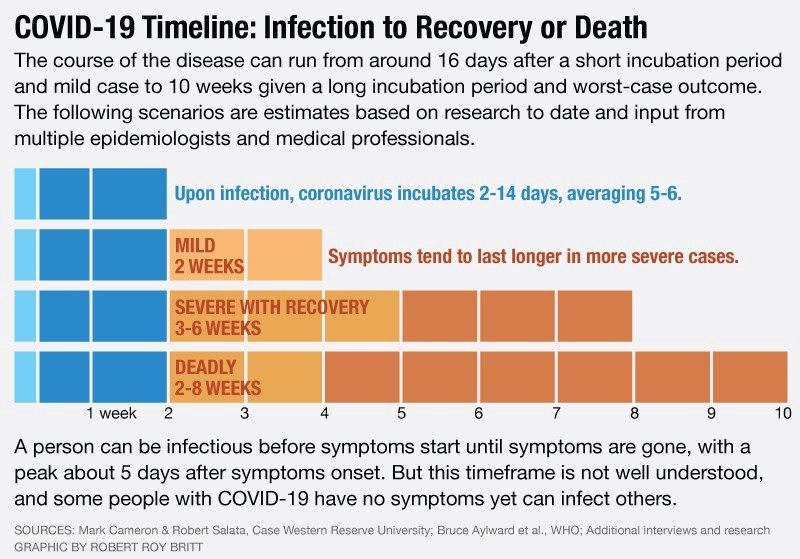
3. Finalmente, hemos seleccionado una publicación científica por tratar de dar más rigor al análisis (Robert et al. Estimates of the severity of coronavirus disease 2019: a model-based analysis. The Lancet Infectious Diseases, Volume 20, Issue 6, 669 – 677). En este estudio se estima que el tiempo que transcurre desde que aparecen síntomas hasta que una persona fallece está entre 16.9 y 19.2 días con un 95% de probabilidad.

En resumen…

… Tenemos tres fuentes que nos dicen que los tiempos desde el contagio hasta el fallecimiento oscilan en las siguientes bandas:

• 21-25 días.
• 14-28 días, pero algunos pueden tardar hasta 10 semanas en fallecer.
• 18.9-33.2 días que resultan de sumar a la banda de confianza del 95% (16.9,19.2) del tiempo desde que aparecen síntomas hasta que fallecen, al que le sumamos el periodo de incubación desde el contagio hasta que se presentan síntomas, de 2 a 14 días con una media entre 5 y 6.

Con esta información y la del MOMO vamos a representar los datos de fallecidos diarios y las bandas que se corresponden con sumarle al 8 de marzo los 3 rangos que hemos obtenido de las tres fuentes diferentes. Los resultados se muestran en las 5 gráficas siguientes para las comunidades más afectadas y para España en su conjunto:

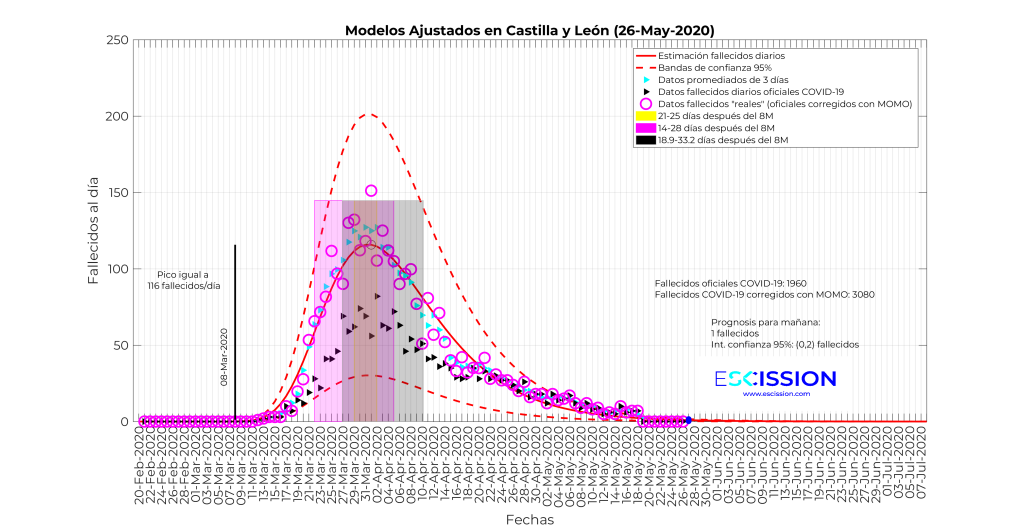
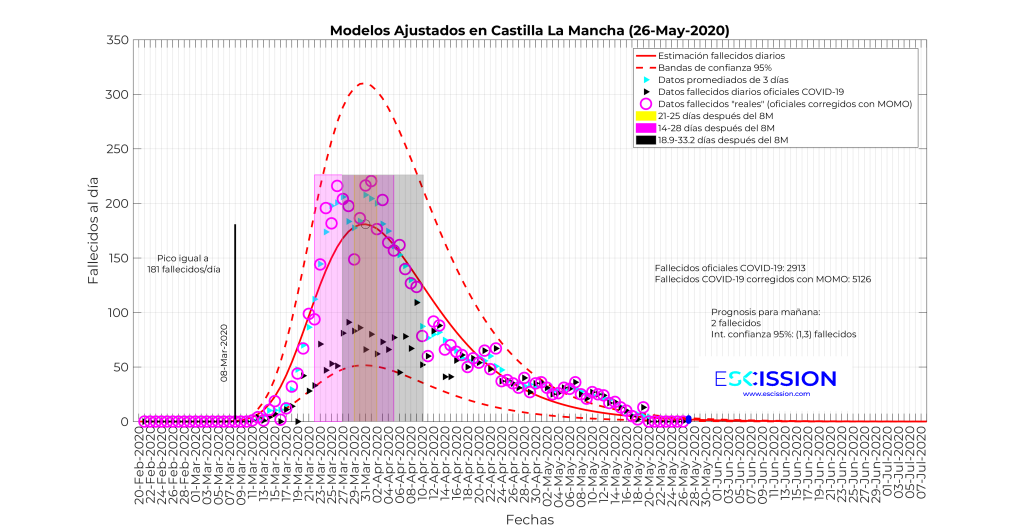
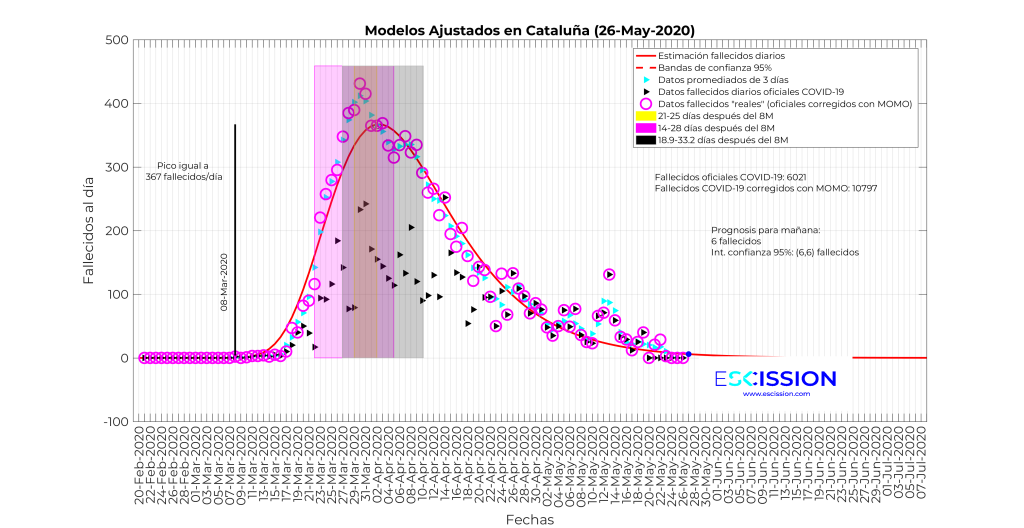
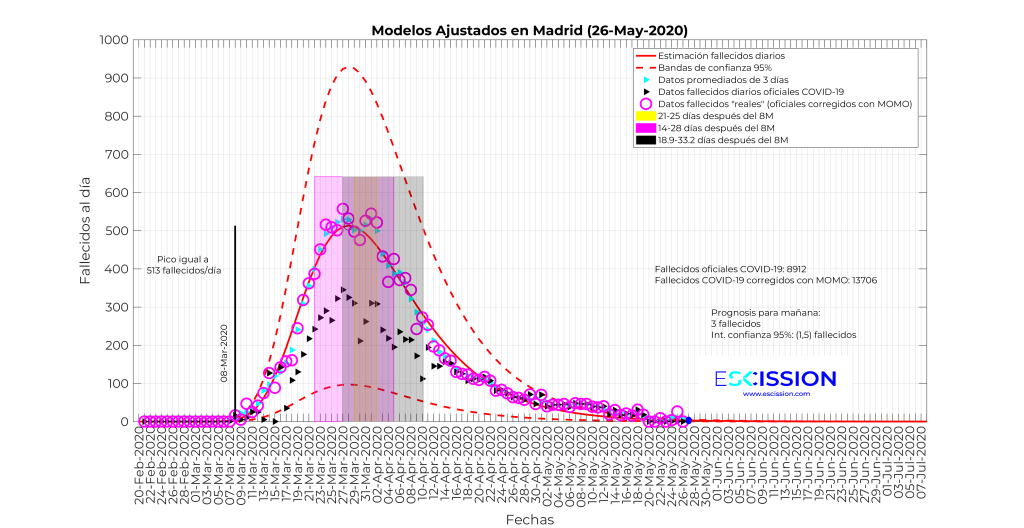
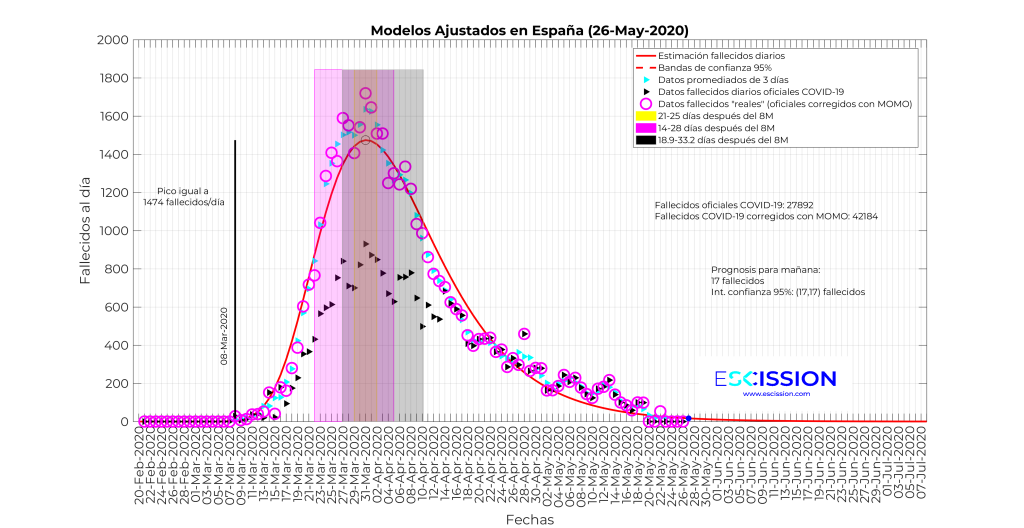
La mera observación de estas tres gráficas permite extraer las siguientes conclusiones preliminares:

1. Los fallecidos por COVID-19, de acuerdo con el sistema MOMO, son muchos más de los que figuran en las cifras oficiales, lo cual parece obvio día de hoy y ya se han hecho eco distintos medios de comunicación. Nosotros ofrecemos una estimación rigurosa acorde con los datos disponibles.
2. Visualmente, las ventanas de tiempo en las que una persona contagiada en 8 de marzo fallecería se corresponden con los picos de fallecimientos por COVID-19 diarios. Nótese que las tres bandas se superponen y eso dificulta su identificación visual, pero permiten comprobar en todo caso su coincidencia con el pico.

Sin embargo…

Este análisis sigue teniendo una connotación un tanto subjetiva. Por ese motivo vamos a tratar de ir un poco más allá reproduciendo la curva de contagio de las personas que han fallecido. Lo vamos a hacer a nivel nacional, y para ello vamos a hacer las siguientes consideraciones:

1. Los extremos de las ventanas de las tres fuentes consultadas que marcan el tiempo desde que una persona se contagia hasta que fallece son 14 y 33.2 días. Asumiendo una distribución normal y que la probabilidad de que el tiempo de fallecimiento esté entre 14 y 33.2 sea del 95%, los parámetros de la distribución resultan en una media de 23.6 días y una desviación típica de 4.9 días:

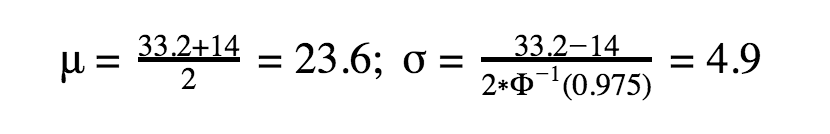
A pesar de esto, también se sabe que la distribución de probabilidad tiene un coeficiente de asimetría positivo, por lo que situaremos la media en un valor ligeramente más bajo μ=22. Además, emplearemos la distribución lognormal para reproducir esa asimetría positiva, cuyos parámetros se obtienen en función de la media y la desviación típica en el espacio original de la siguiente manera:

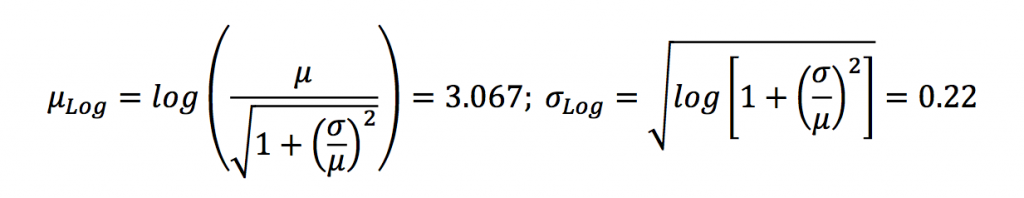
2. El número de personas contagiadas en el día 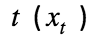que posteriormente fallecen va a ser igual a .

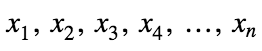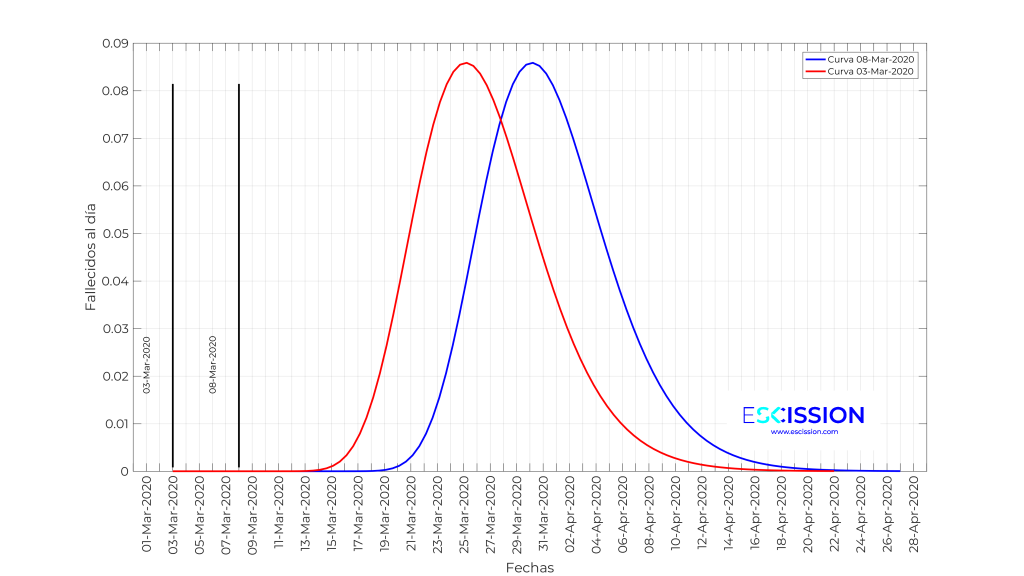
3. Si tenemos 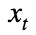contagiados en un día t, los fallecimientos por COVID-19 en los días siguientes se van a distribuir de acuerdo con la distribución logarítmico normal definida anteriormente. Así, para un contagiado el día 8 de marzo la distribución de probabilidad de cuando se produciría su fallecimiento se corresponde con la curva azul mostrada en la siguiente figura, y para otro fallecido en el día 3 de marzo lo haría con la roja. Es una mera translación de la curva patrón.

4. Las curvas anteriores definidas como 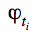nos permiten saber para cada día t el número de fallecidos que proceden de los 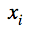contagiados del día 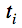de la siguiente manera:

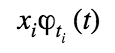
5. Para cada día t, el número de fallecidos 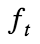se obtiene de sumar los fallecidos que proceden de contagios en todos los días anteriores:

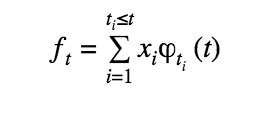
6. Para tratar de generar una curva suave pero además permitir que esa curva tenga discontinuidades (saltos discretos) en fechas concretas, los contagiados para cada día se definen por las curvas mostradas en la siguiente figura, de forma que las variables de decisión se reducen a los parámetros de las curvas:

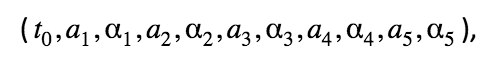
Mientras que el resto de parámetros 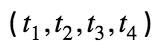se corresponden con las fechas que se quieren analizar: el 8 de marzo por los eventos que supusieron aglomeraciones de gente (congreso de VOX, las manifestaciones, …), el 15 de marzo por la declaración del estado de alarma, el 30 de marzo por el aumento de la dureza del confinamiento permitiendo sólo actividades denominadas esenciales, y el 11 de abril por la vuelta a la situación anterior al 30 de marzo. De esta manera queremos comprobar cómo se comporta el modelo en cuanto a la evolución de contagiados.

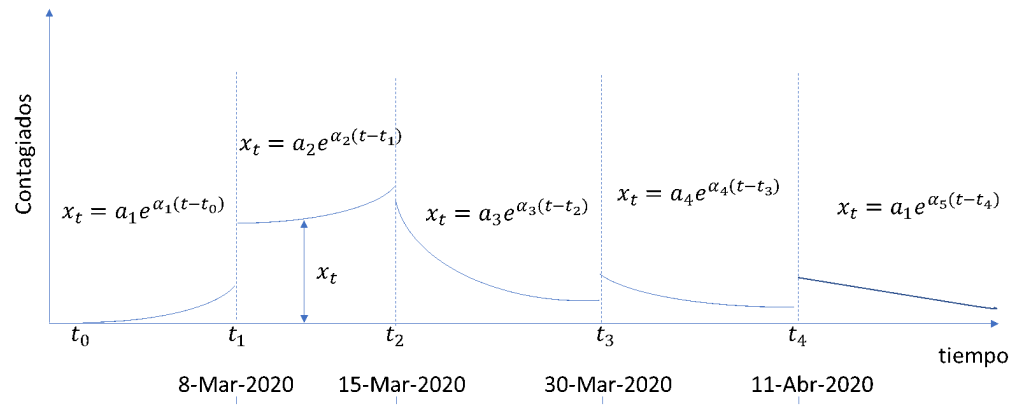
La motivación para seleccionar tramos de curvas exponenciales es que el modelo exponencial se emplea para crecimiento acumulado descontrolado de pandemias y poblaciones, y su derivada continúa siendo exponencial. En este caso, la posibilidad de usar tramos diferentes y exponentes negativos permite modelar no sólo crecimientos sino decrecimientos.

7. Con toda esta información, solo resta resolver un problema de estimación de contagiados para cada día, que se hace minimizando la suma de los residuos al cuadrado:

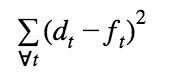
Donde 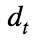son los datos de fallecidos diarios del MOMO, y 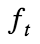son los datos estimados en función de los contagiados estimados. Nótese que se trata de un ajuste por mínimos cuadrados, que asumiendo la hipótesis de normalidad de los residuos, se corresponden con el estimador de máxima verosimilitud. Lo que pretendemos es tratar de reproducir la evolución más probable de la curva de contagios asociada a los fallecidos.

Si hacemos ese ejercicio para el conjunto de España…

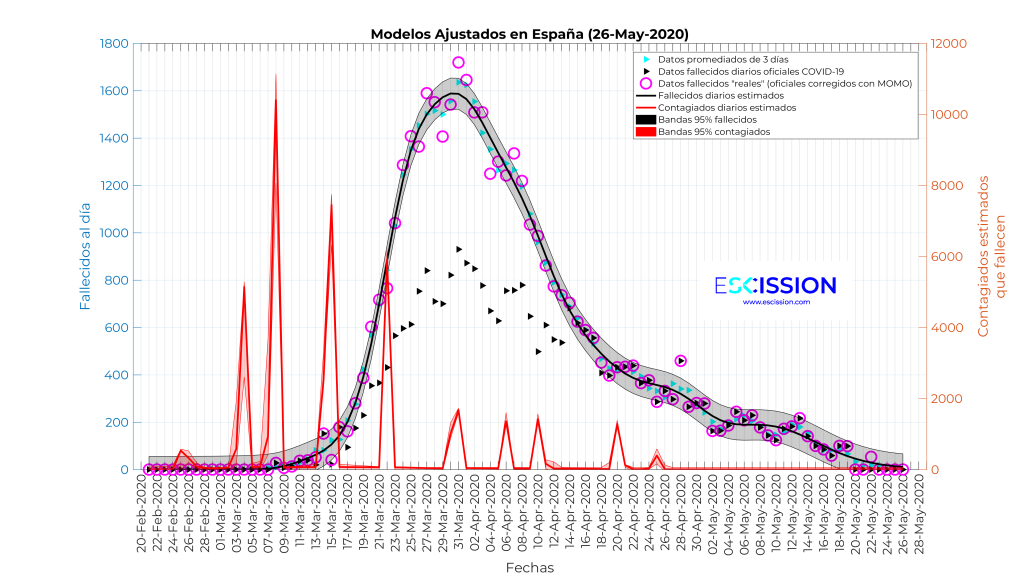
… Se obtiene el resultado que se muestra en la figura abajo mostrada. Nótese que la estimación de fallecidos es muy precisa, con unas bandas de confianza muy estrechas, lo cual evidencia que la parametrización escogida reproduce de forma muy fiel la realidad observada. El área bajo la curva roja es igual al área bajo la curva negra, y nótese también que se han empleado dos escalas verticales diferentes a la izquierda y a la derecha del gráfico. Asimismo se puede ver que, si el tiempo desde el contagio hasta el fallecimiento fuera una constante, la curva roja sería una mera traslación de la curva negra igual al tiempo de fallecimiento. Sin embargo, para ser capaces de reproducir la curva “real” de fallecidos tenemos el siguiente comportamiento de la curva de contagio:

1. La curva de contagio crece exponencialmente desde el 20 de febrero hasta alcanzar el pico máximo de 4591 contagiados el 8 de marzo, lo cual es comportamiento normal cuando no hay medidas para evitar el contagio. 
2. El día 9 de marzo desciende bruscamente y aumenta de forma gradual hasta el día 15 de marzo, en el que se declara el estado de alarma.
3. A partir del estado de alarma la curva de contagios entra en clara recesión, con dos ligeros repuntes el 30 de marzo y el 11 de abril. Esos repuntes han sido los responsables de que los datos de fallecidos diarios en las dos primeras semanas de mayo no terminaran de irse a cero.

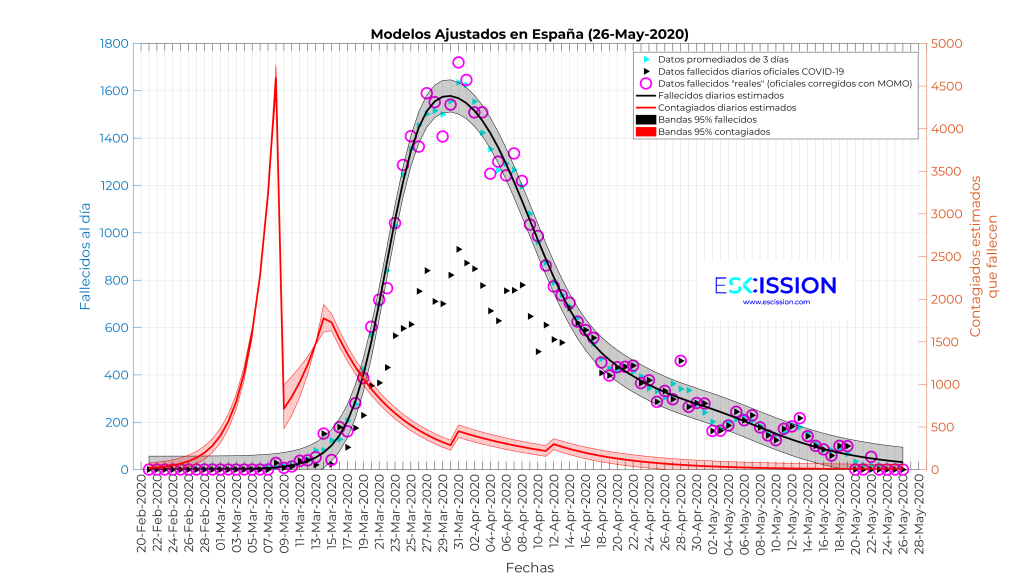
Si analizamos objetivamente estas curvas parece evidente que el 8M tuvo influencia, si no fuera así, el primer tramo de la curva desde el 20 de febrero hasta el 15 de marzo habría tenido un crecimiento exponencial con una única curva común. La única duda que nos queda es cuantificar su efecto, lo cual es complicado porque la supresión del 8M afectaría a toda la curva de contagios y fallecidos. Como mínimo, le podemos achacar los 4591 fallecidos del pico de ese día.

Sin embargo, nos parece incluso más razonable cuantificar su efecto como el área rayada que resulta de prolongar el tramo de curva entre el 8M y el 15M hacia atrás hasta que intercepte la curva actual, tal y como se muestra en la siguiente figura. En ese caso, estamos hablando de 12161 fallecidos directamente achacables al 8M.

Con el propósito de hacer un modelo alternativo…

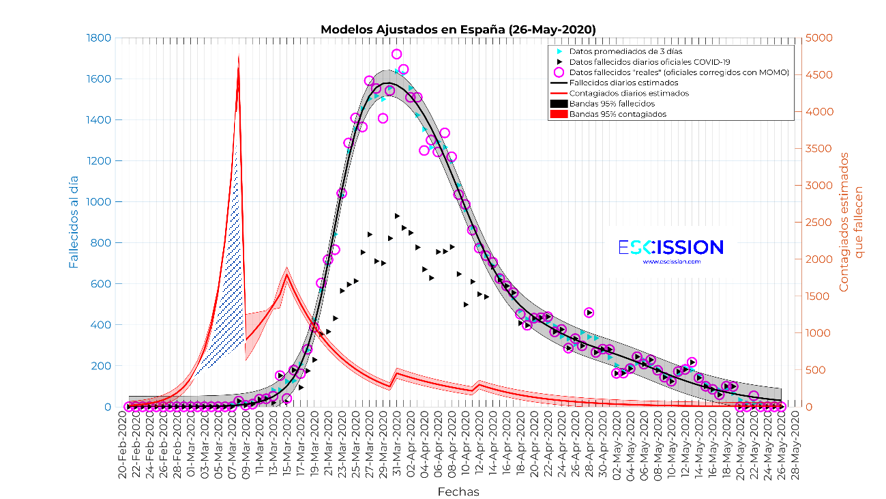
… También consideramos la posibilidad de ajustar una curva continua de Bertalanffy y Richards (la que empleamos para el ajuste de fallecidos en los estudios que hemos hecho) con la posibilidad de incorporar fallecidos adicionales en las fechas seleccionadas. En este caso, el resultado es el que se muestra en la siguiente figura. Nótese que sólo añade fallecidos adicionales en el 8 de marzo y el 11 de abril, pero no considera ninguno el 15 de marzo. En este caso, el número mínimo de fallecidos asociados al 8 de marzo es de 6083. Nótese que el pico del 11 de abril es responsable de la joroba de los fallecidos ajustados 3 semanas después, análogamente, el pico del 8 de marzo es el responsable de la joroba asociada a la punta de fallecidos diarios. Podría incluso parecer que los datos oficiales (triángulos negros) son el resultado de eliminar el efecto del 8 de marzo.

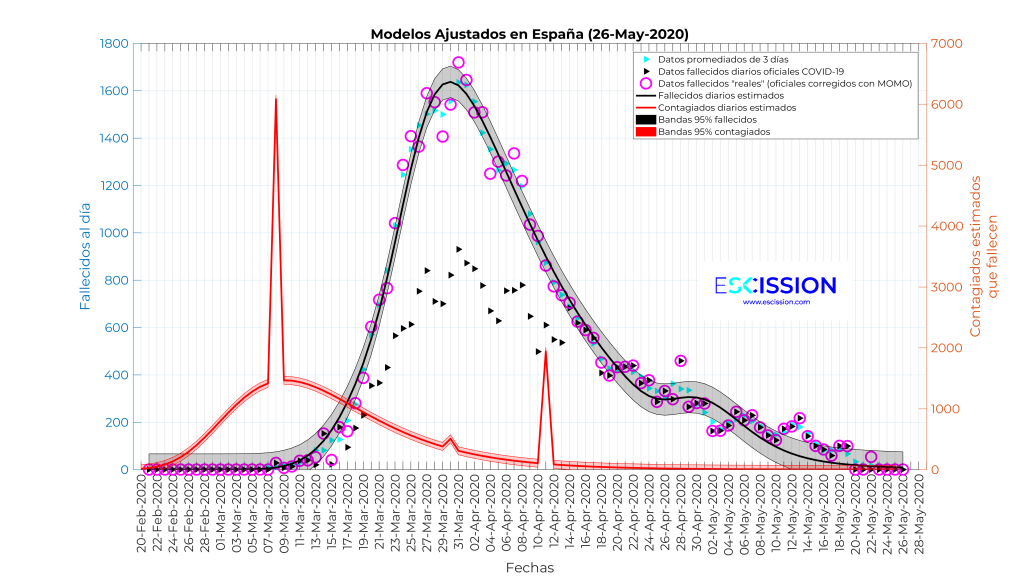
Sin embargo, alguien podría pensar que el seleccionar de antemano los días en los que se permiten generar discontinuidades en los datos precondiciona el resultado. Por eso, hemos resuelto el problema de estimación de nuevo pero, en lugar de emplear las funciones a trozos, o la combinación de una curva continua y valores discretos en fechas señaladas, empleamos como variables de decisión los contagiados de cada día. El resultado en este caso se muestra en la siguiente figura, en la que los contagios se concentran en días concretos, situando los dos mayores picos el 8 y el 15 de marzo, con 10397 y 7448 contagiados respectivamente. Por lo tanto, en este caso hablamos de 10397 fallecidos ligados al 8 de marzo.

En definitiva…

• Usando distintos modelos alternativos llegamos siempre a la conclusión de que el 8M tuvo influencia, lo cual es obvio a día de hoy teniendo en cuenta la capacidad de transmisión que tiene el virus si no se guardan las distancias.
• Cuantificar de forma precisa su magnitud es más complejo pero la menor de las estimaciones es de 4591 fallecidos. Nótese que estamos empleando los datos del MOMO que exceden del quantil del 99%, pero lo más adecuado sería emplear los datos que exceden de la media, con lo cual el número de fallecidos aumentaría.
• Este último punto no estaba en la versión inicial del artículo y lo añado como aclaración por un comentario que me han hecho sobre mi artículo inicial y que me parece pertinente puntualizar. El estudio analiza el 8 de marzo en su conjunto, y si bien las manifestaciones del 8 de marzo pudieron producir las mayores congregaciones de gente y por lo tanto tener más influencia, no le resta importancia al hecho de que habría sido muchísimo más beneficioso para todos que no se hubiera permitido ninguna concentración de gente de ningún tipo en esa fecha.
• Por último resaltar que en caso de futuros brotes es importante evitar el efecto pánico que ciertas decisiones pueden generar, ya que nos ha llamado la atención el repunte asociado al 15 de marzo, posiblemente motivado por la histeria colectiva tras la notificación de que se iba a activar el estado de alarma, y que indujo a muchos ciudadanos a acudir en masa a los supermercados para aprovisionarse.

Os agradeceríamos que compartierais con nosotros vuestras opiniones, críticas o vuestra propia interpretación de los datos y/o del análisis que proporcionamos. Lo podéis hacer bien vía LinkedIn, a través de nuestra cuenta de Twitter, o en nuestro formulario de contacto.

REFERENCIAS BIBLIOGRÁFICAS Y ENLACES WEB

• https://www.cope.es/emisoras/castilla-la-mancha/ciudad-real-provincia/ciudad-real/noticias/parece-que-hemos-llegado-pico-fallecimientos-diarios-clm-ahora-esa-curva-deberia-descendiendo-20200331_663872
• https://www.rtve.es/alacarta/videos/noticias-de-castilla-la-mancha/clm-20200408135701ok/5554055
• https://elemental.medium.com/from-infection-to-recovery-how-long-it-lasts-199e266fd018
• Robert et al. Estimates of the severity of coronavirus disease 2019: a model-based analysis. The Lancet Infectious Diseases, Volume 20, Issue 6, 669 – 677.
• F. J. Richards. A flexible growth function for empirical use. J. Exp. Bof., 10:290, 1959.
• M. E. Turner, E. L. Bradley, and K. A. Kirk. A theory of growth. Mathematical Biosciences, 26:367–373, 1976.
• P. F. Verhulst. Notice sur la loi que la populationsuit dans son accroissement. Corr. Math. Phys., 10:113, 1838.
• L. von Bertalanfy. Untersuchungen uber die gesetzlichkeit des wachstums, VII, stofwechseltypen und wachstumstypen. Biol. Zentralbl., 61:510, 1941.