¿Funcionan las vacunas?
Esta es la pregunta del millón, ¿funcionan las vacunas? En nuestro caso tenemos dudas fundadas sobre el efecto positivo real que están teniendo, especialmente ante esta nueva ola de contagios por la nueva variante Omicron. Sin embargo, un altísimo porcentaje de la población tiene clarísimo que las vacunas funcionan. No tenemos claro si se debe a la insistencia que ponen los medios de comunicación en repetir frases como: “…menos mal que gran parte de la población está vacunada, si no…”, “…un claro descenso del número de fallecidos gracias a las vacunas…”, o si sin embargo se debe al deseo que tiene toda la gente que se ha vacunado de que realmente funcione, incluidos nosotros.
¿Cuál es el propósito de este artículo? Hacer una análisis objetivo basado en los datos para tratar de dar un criterio racional para determinar si las vacunas están teniendo realmente un efecto positivo, o si por el contrario no lo están teniendo. Nuestros gobernantes han confiado a las vacunas la solución de la pandemia y es fundamental detectar lo antes posible si realmente están ayudando, o si meramente van a prolongar nuestra agonía.
En esta tarea nos vamos a ayudar de un modelo matemático conceptualmente sencillo, pero que nos va a permitir juzgar con mayor objetividad el efecto de las vacunas en la tasa de fallecimiento por COVID-19.
Modelo de previsión de fallecimientos en función de los positivos
El presente documento muestra los resultados de un modelo matemático sencillo con dos parámetros que permite comprobar el ajuste de la estimación de fallecidos por COVID en función de los positivos por PCR. Los dos parámetros del modelo son:
- Desfase: Este parámetro controla el tiempo medio que transcurre desde que se identifica un positivo hasta que se produce el fallecimiento.
- Tasa de mortalidad: Porcentaje de contagiados que fallece.
Antes de analizar el resultado hay que tener las siguientes consideraciones:
- No incluimos datos anteriores al 21 de junio de 2020 porque no se realizaban PCRs y el número de contagiados está claramente infravalorado con respecto a la situación posterior a esa fecha.
- Asumimos que la cifra de muertos por COVID es real, y que los criterios de clasificación de fallecimiento por COVID son constantes en todo el periodo de análisis.
- Asumimos que el porcentaje de positivos detectados oficiales es proporcional al porcentaje real en todo el periodo de análisis, lo cual puede no ser cierto. Es muy complicado saber si el número de contagiados real es mucho mayor a las cifras proporcionadas, en este sentido las tasas obtenidas se pueden asumir cotas superiores.
El propósito que nos planteamos es relacionar los fallecidos para los próximos días con la información de contagiados detectados. Para ello vamos a partir de los siguientes supuestos, todos ellos refrendados por los datos e información científica especializada (consulta nuestra entrada del blog de 8 de marzo):
- El número de personas que fallecen (
), es un porcentaje del número de personas que se contagian (
).
- Si tenemos
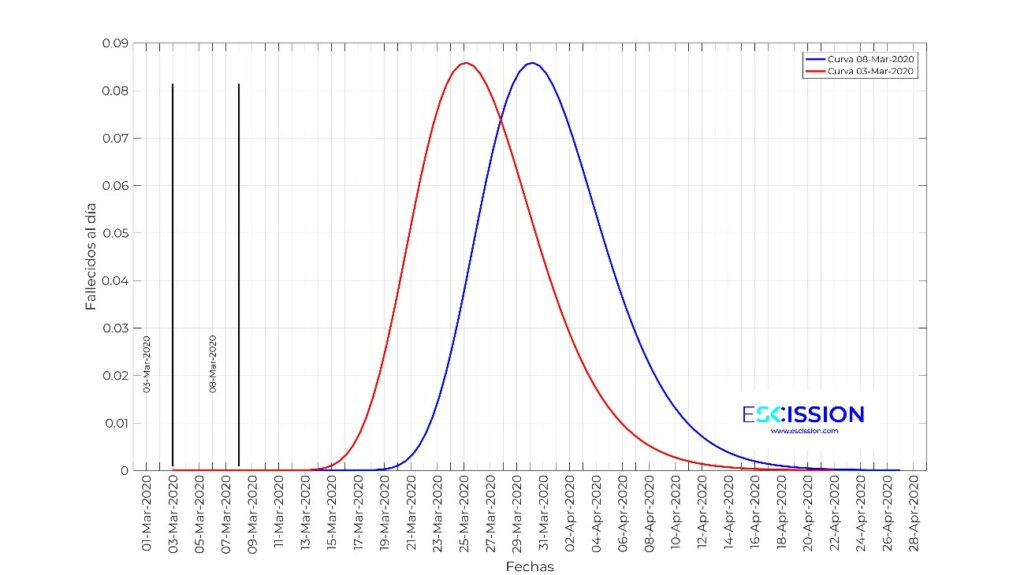
contagiados en un día t, los fallecidos (un porcentaje de los contagiados) en los días siguientes se van a distribuir de acuerdo con una distribución logarítmico-normal como la mostrada en la siguiente figura. Así, para un contagiado el día 8 de marzo, la distribución de probabilidad de cuando se produciría su fallecimiento se corresponde con la curva azul mostrada en la siguiente figura, y para otro fallecido en el día 3 de marzo lo haría con la roja. Es una mera translación de la curva patrón. Esa curva patrón tiene dos parámetros que la definen: la media y la desviación típica de la distribución. Nótese que la media se desfasa con respecto a la fecha de contagio, y ese desfase es un parámetro a determinar en el modelo. Nótese que la desviación típica se iguala al desfase para que sólo haya dos parámetros en el modelo.
- Las curvas anteriores definidas como
nos permiten saber para cada día t el número fallecidos estimados
(de ahí la tilde en la expresión) que proceden de los contagiados
del día
de la siguiente manera:
.
- Para cada día t, el número de fallecidos
estimados se obtiene de sumar los fallecidos que proceden de contagios en todos los días anteriores:
.
- Con toda esta información, solo resta resolver un problema de estimación de parámetros minimizando la suma de los residuos al cuadrado entre las observaciones y las predicciones con el modelo en función de los contagiados.
En primer lugar aplicamos el modelo a los datos sin discriminación por sexo o edad. Los resultados se muestran en la siguiente figura, en la que observamos los siguientes elementos:
- Los puntos circulares rojos son positivos declarados oficiales por día, su magnitud se indica en el eje vertical de la derecha.
- Los puntos triangulares azules muestran los fallecidos oficiales por COVID diarios.
- La línea azul es el resultado de aplicar a los puntos rojos el resultado del modelo, para ello empleamos mínimos cuadrados para estimar los parámetros. El sombreado azul representa las bandas de confianza.
- El modelo estima una única tasa de fallecimiento del 1,23% y un tiempo medio entre contagio y fallecimiento de 17,8 días.
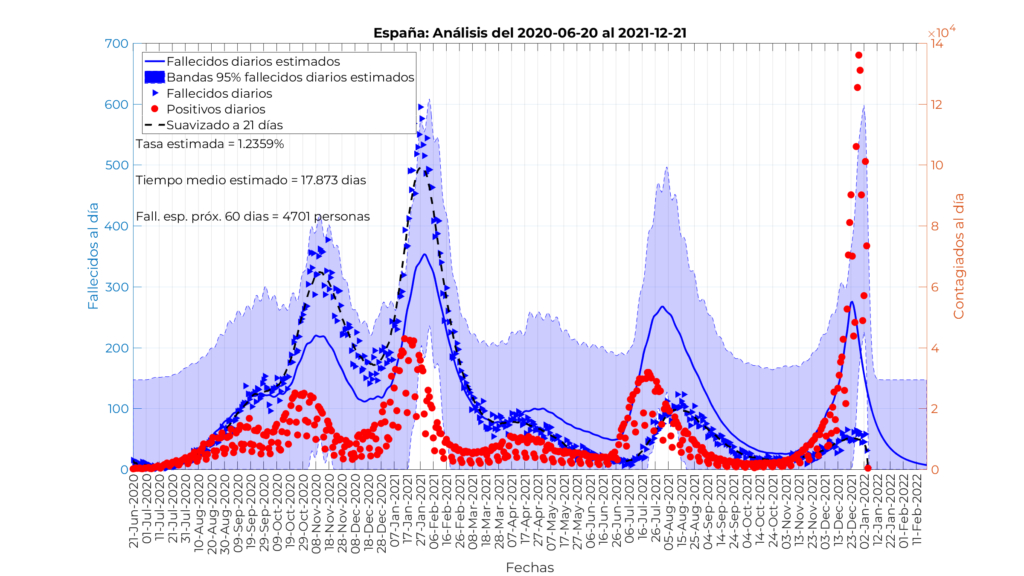
Si nos centramos en el resultado observamos que un único ajuste no es posible, ya que el modelo parece infravalorar los fallecidos antes del 10 de abril aproximadamente, y los sobrevalora a partir de esa misma fecha. Otro punto que perturba el modelo en la nueva variante Omicron , que está generando un número de contagios sin precedentes y que claramente tiene un comportamiento diferente en términos de letalidad. Para evitar que este efecto contamine el modelo vamos a hacer el análisis usando datos del 21 de junio de 2020 al 21 de diciembre de 2021.
No sería descabellado pensar que esa disminución de la tasa de mortalidad sea debida a las vacunas, lo cual supondría que las vacunas reducen la tasa de mortalidad en bastante más del 50%. Estos datos, asumiendo que se cumplen las hipótesis mencionadas anteriormente, apoyan el beneficio de la vacuna en términos de reducción de mortalidad.
Sin embargo, y dado que es claro que la tasa de mortalidad varía sustancialmente en función del rango de edad, vamos a proceder a hacer el mismo análisis por franjas de edad. Y lo vamos a empezar a hacer por las franjas más vulnerables.
Modelo para mayores de 79 años
El resultado se muestra en la siguiente figura, con una tasa de mortalidad estimada del 16% y un tiempo medio desde el contagio hasta el fallecimiento de 12,8 días:
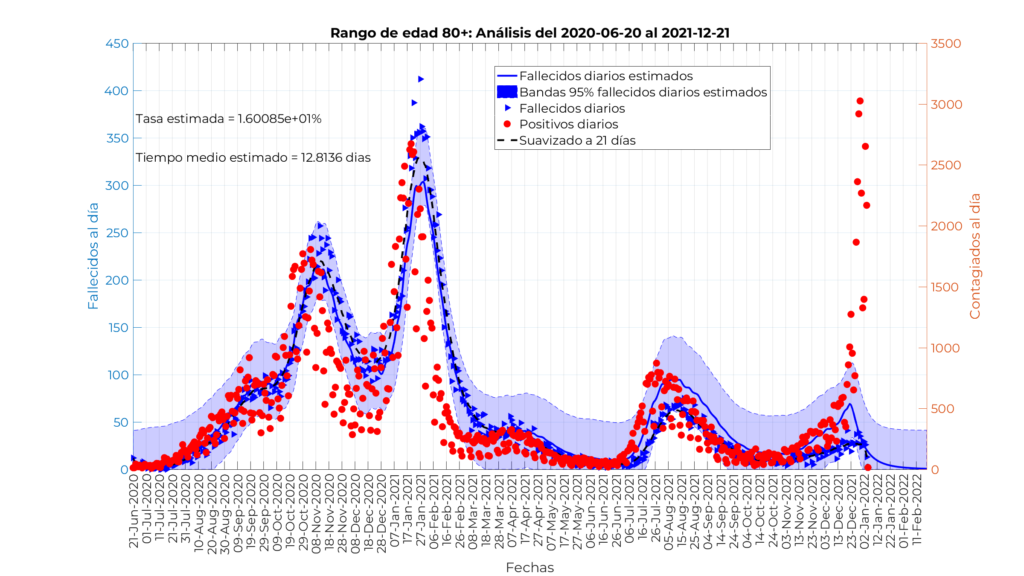
En este caso el ajuste del modelo es muy bueno hasta el 10 de abril aproximadamente, con muy poca dispersión en torno a la media. A partir de ese momento los fallecidos reales están ligeramente por debajo de los pronosticados por el modelo, sin embargo la reducción en la tasa de mortalidad es mucho menor de ese más del 50% que habíamos estimado inicialmente sin discriminación por edad.
Podemos observar también cómo el efecto Omicron perturba el modelo con un incremento brutal de los contagiados a partir de diciembre de 2021 que no se ve acompañado por los fallecidos, lo cual confirma la hipótesis de que esta variante es menos agresiva. Este cambio de tendencia hace que sea necesario no utilizar datos más allá del 21 de diciembre para no perturbar el resultado añadiendo datos que claramente no cumplen con las hipótesis del modelo de partida.
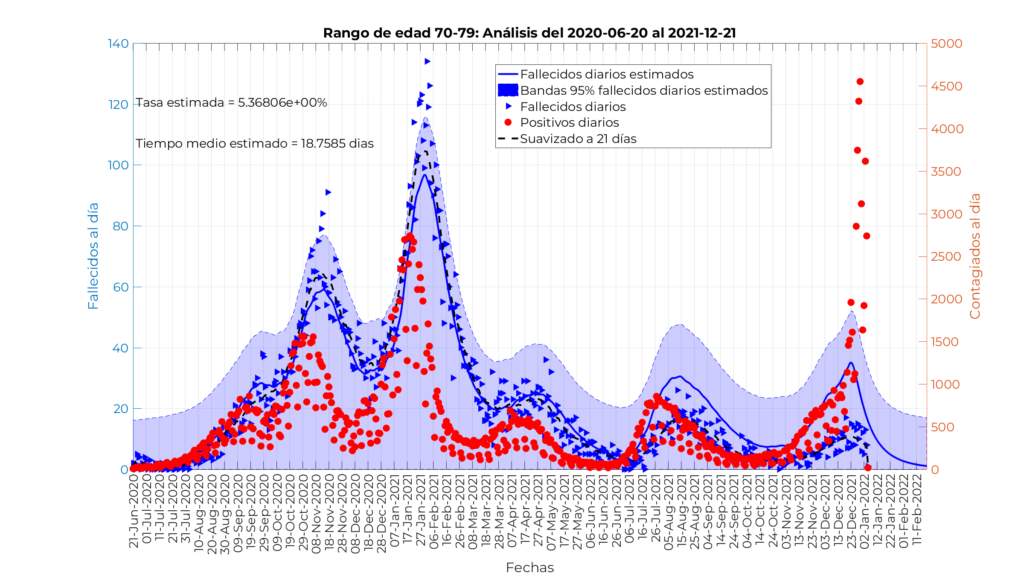
Modelo para personas entre 70 y 79 años
En este caso el ajuste del modelo es también bastante bueno hasta el 10 de abril aproximadamente, con muy poca dispersión en torno a la media aunque un poco más que en el caso de mayores de 79 años. La tasa de mortalidad estimada es del 5,4% , mucho menor que en la franja de edad superior, y un tiempo medio desde el contagio hasta el fallecimiento de 18,76 días. A partir del 10 de abril, los fallecidos reales están ligeramente por debajo de los pronosticados por el modelo, pero análogamente al caso anterior la reducción en la tasa de mortalidad es mucho menor de ese más del 50% que habíamos estimado inicialmente.
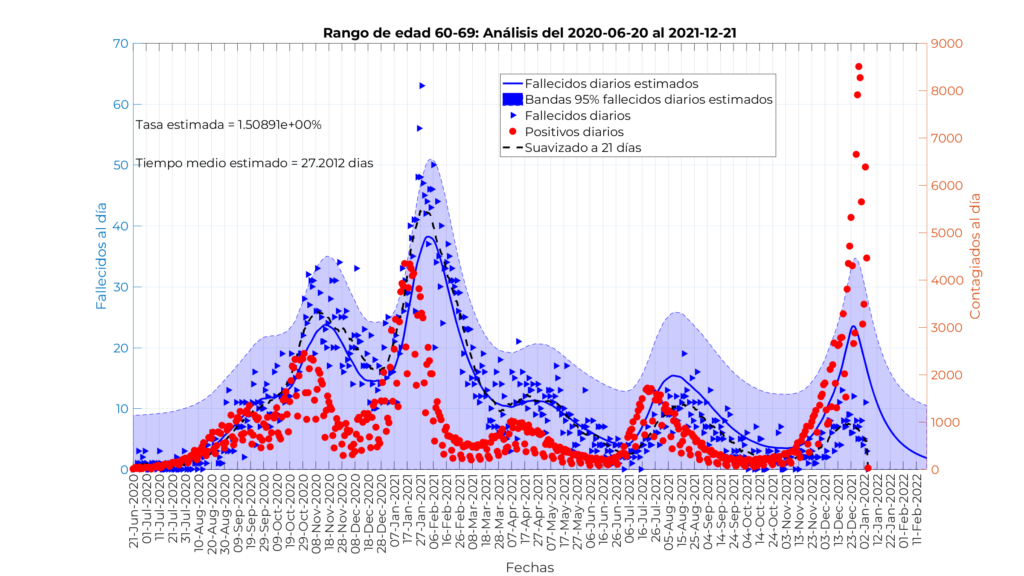
Modelo para personas entre 60 y 69 años
En este caso el ajuste del modelo es también bastante bueno hasta el 10 de abril aproximadamente, con muy poca dispersión en torno a la media aunque un poco más que en el caso de mayores de 69 años. La tasa de mortalidad estimada es del 1,5% , mucho menor que en la franja de edad superior, y un tiempo medio desde el contagio hasta el fallecimiento de 27,2 días. A partir del 10 de abril, la media de los fallecidos reales está ligeramente por debajo de la media pronosticada por el modelo, pero esa reducción es incluso menor que en caso anterior.
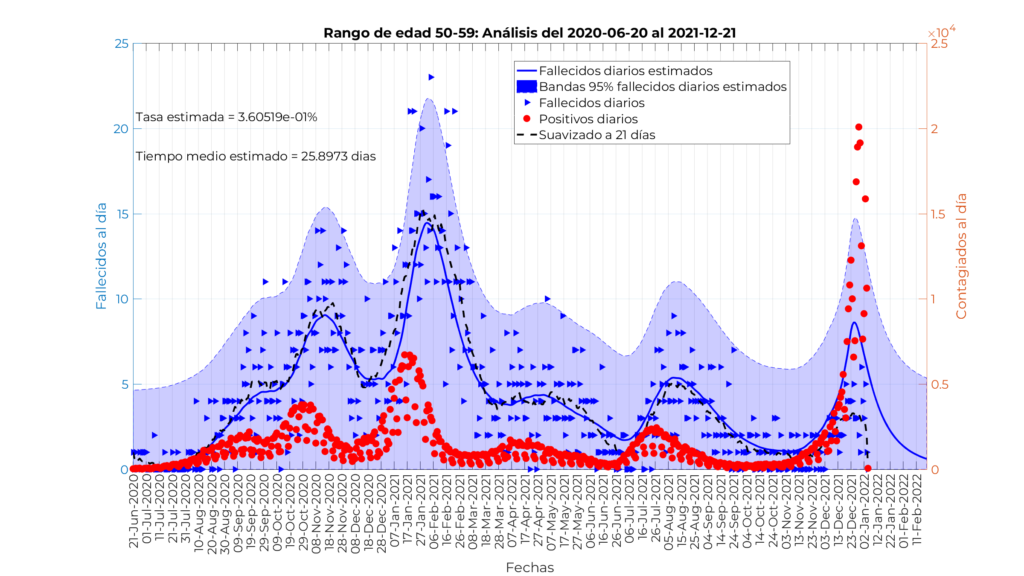
Modelo para personas entre 50 y 59 años
En este caso el ajuste del modelo es también bastante bueno, aunque con mucha más dispersión. Este comportamiento es razonable de acuerdo con el teorema central del límite, ya que el porcentaje de fallecidos aumenta exponencialmente con la edad y cada vez hay menos fallecidos y aumenta la incertidumbre. En este caso ya no hay una distinción clara de dos periodos, por lo que es más complicado corroborar las bondades de las vacunas como reductoras de la letalidad frente al COVID en esta franja de edad. Nótese cómo el modelo reproduce muy bien la media suavizada a 21 días de los datos empíricos. La tasa de mortalidad estimada es del 0,36% , mucho menor que en la franja de edad superior, y un tiempo medio desde el contagio hasta el fallecimiento de 25,9 días.
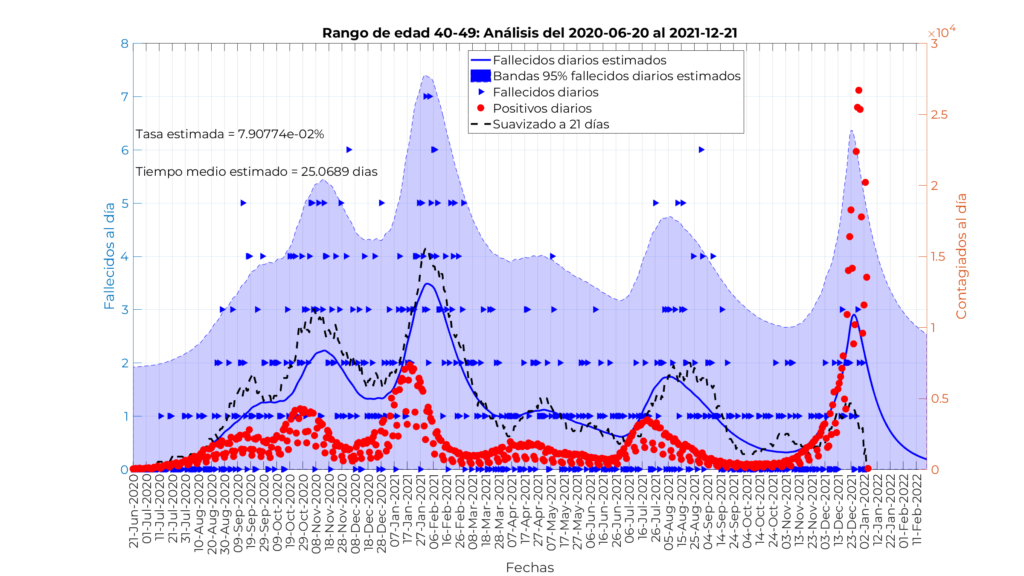
Modelo para personas entre 40 y 49 años
La pauta que ya hemos observado se confirma en esta franja de edades, aumenta la dispersión con respecto a la media, y no se aprecia un efecto positivo significativo en términos de tasas de mortalidad. Nótese cómo el modelo reproduce muy bien la media suavizada a 21 días de los datos empíricos. La tasa de mortalidad estimada es del 0,079% , mucho menor que en la franja de edad superior, y un tiempo medio desde el contagio hasta el fallecimiento de 25,1 días.
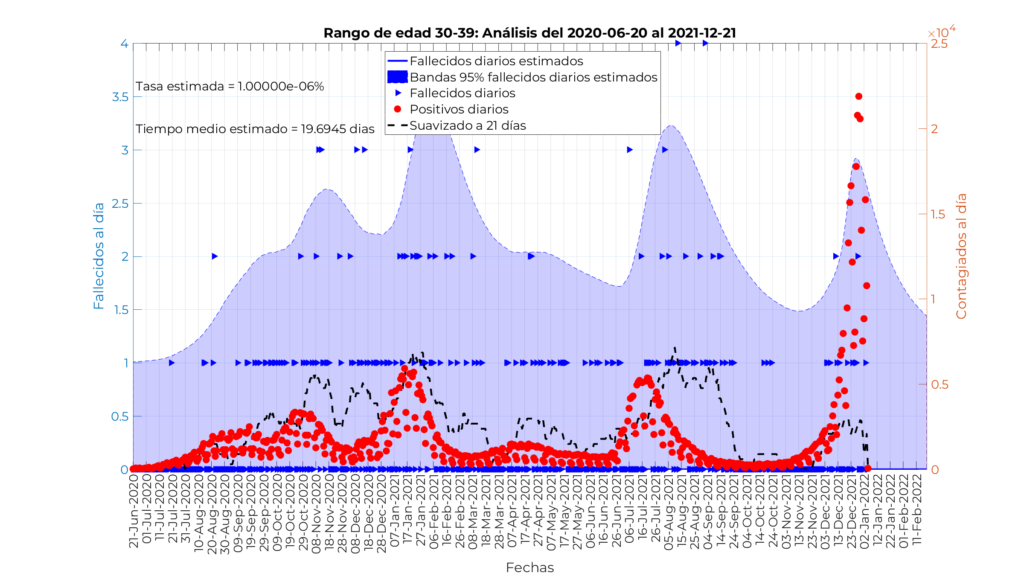
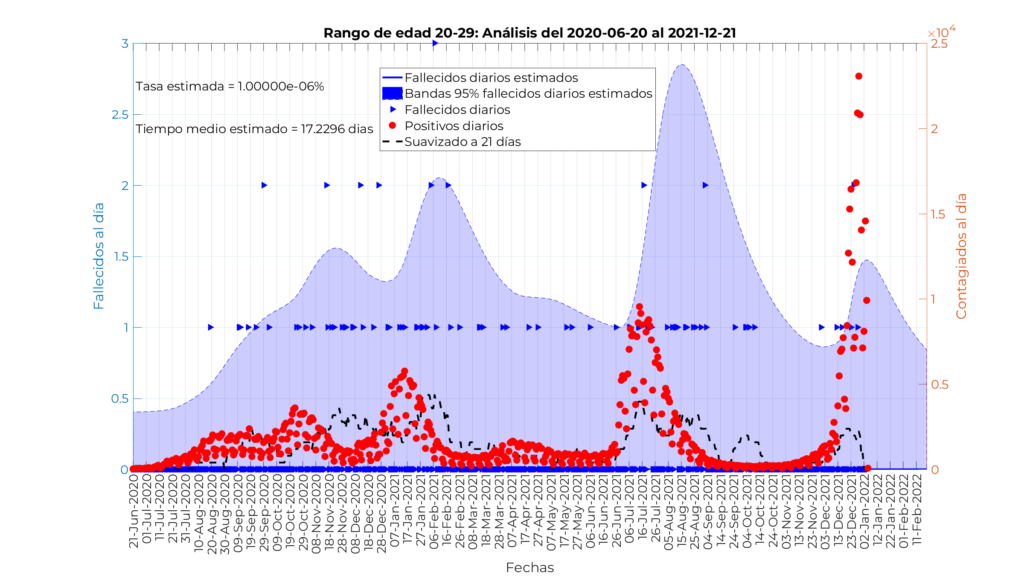
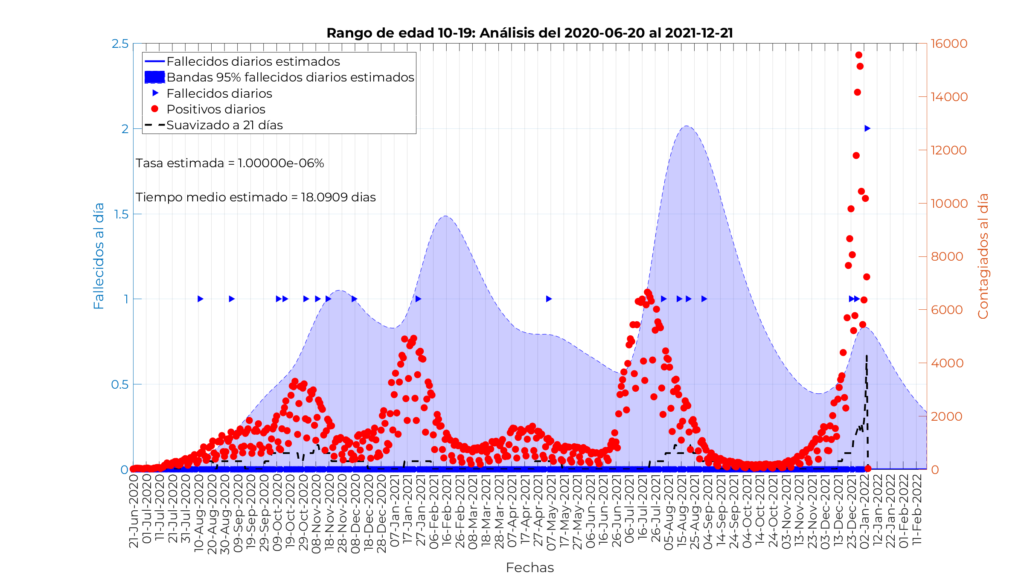
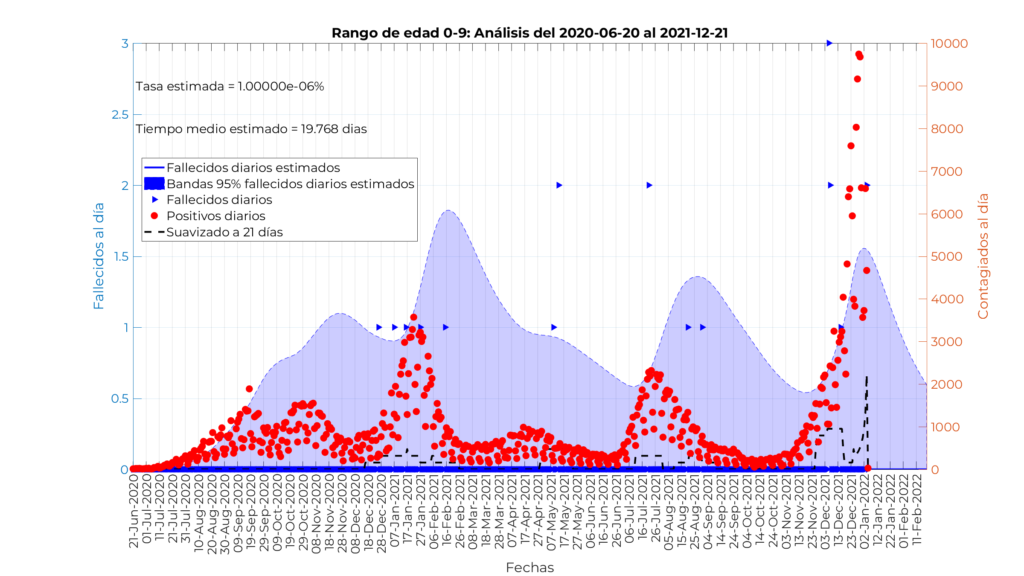
Modelo para personas menores de 40 años
En este caso presentamos los resultados de los tres modelos de forma simultánea, ya que su interpretación es muy similar. Nótese que la tasa de mortalidad estimada es tan pequeña que el valor estimado por el modelo no se despega de los 0 fallecimientos por día. La tasa estimada se ha ido al valor mínimo establecido en el procedimiento de optimización, y los tiempos medios estimados desde el contagio hasta el fallecimiento se corresponden con de 19,7 días, 19,7 días, 18,1 días, y 19,8 días, respectivamente.
Conclusiones
Los datos oficiales permiten entrever el beneficio de las vacunas en la reducción de la tasa de mortalidad, pero en las edades más vulnerables y siempre teniendo en cuenta las hipótesis que permiten emplear el modelo propuesto.
Otro aspecto que queda claro es la necesidad de discernir y analizar los datos por franjas de edad, porque no hacerlo nos puede llevar a pensar que el beneficio de las vacunas es mayor del que realmente es.
Incoherencia con los datos del MOMO
Antes de analizar los datos del MoMo, es importante describir en qué consiste este sistema. MoMo es un sistema para la Vigilancia de la mortalidad diaria por todas las causas en España. Tiene como objetivo identificar patrones inusuales de mortalidad y estimar el impacto en la mortalidad de la población de cualquier evento de importancia para guiar la acción en Salud Pública.
MoMo se alimenta fundamentalmente de datos de defunciones diarias por todas las causas del Instituto nacional de Estadística (INE), hasta el año en que están disponibles, y de los registros civiles que están actualmente informatizados, desde ese año hasta la actualidad, y que se reciben a través del Ministerio de Justicia.
MoMo se basa en un modelo restrictivo de medias móviles históricas. El modelo compara la mortalidad en cada día del año, en una ventana de +/- 3 días, con la mortalidad observada en los mismos días de los 10 años previos. A partir de esos valores determina el valor esperado (la mediana) y los cuantiles (el intervalo de confianza) A la hora de hacer esta comparación, se ha excluido el periodo del 10 de marzo de 2020 al 31 de diciembre de 2021.
La tendencia se corrige alineando al año 2019 la mortalidad de años anteriores (no se utiliza la mediana del 2020 ni 2021 por posible sobreestimación por la pandemia), utilizando la mediana anual sin outliers. Para ello, se calcula la desviación media con respecto a la mediana de los últimos 10 años, se descartan aquellas observaciones que se desvíen en un factor mayor a 2 con respecto a la mediana, y se calcula de nuevo la mediana.
Para calcular los excesos, esta mortalidad diaria esperada, con sus intervalos de confianza al 99%, se compara con la mortalidad diaria observada procedente de los registros civiles.
Es cierto que los datos oficiales indican una mejora o reducción del porcentaje de fallecidos con respecto a los contagiados, pero el análisis de la información del MOMO también arroja un exceso de mortalidad que no se explica con los fallecidos oficiales por COVID, tal y como se muestra en la figura siguiente. Nótese que desde julio de 2021 los datos oficiales de fallecidos por todas las causas (cuadrados azules) están sistemáticamente por encima de la media, y sin embargo si añadimos a los valores esperados de fallecidos proporcionados por el modelo MOMO, los fallecidos oficiales por COVID, éstos se quedan por debajo de las cifras reales de fallecidos. ¿A qué se deben estas discrepancias?
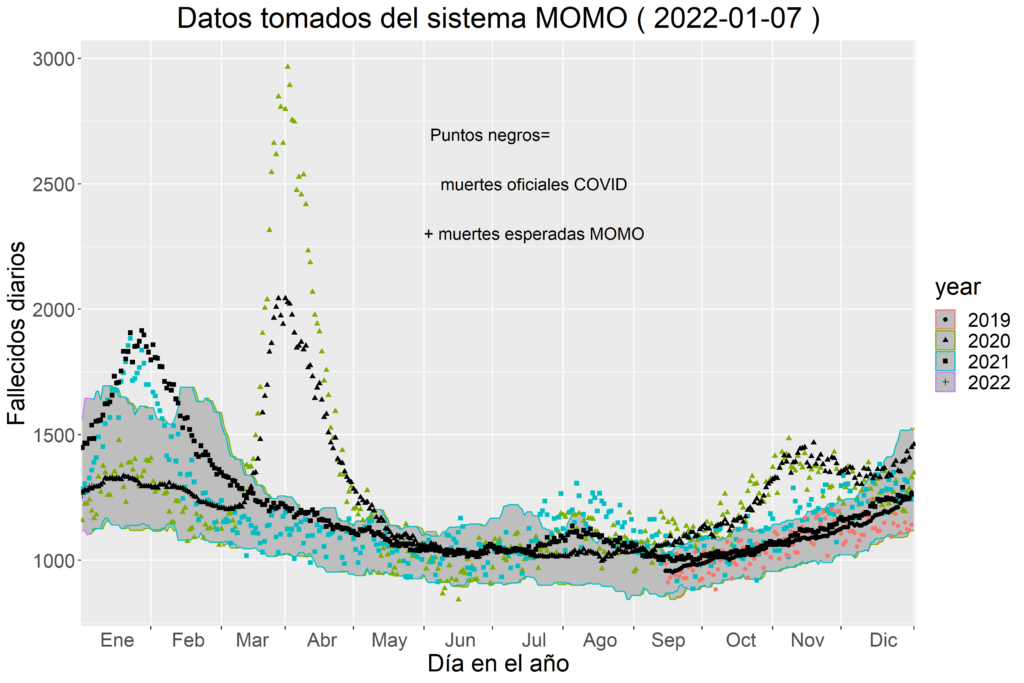
Con el propósito de tratar de explicar o ver si los datos de excesos de fallecidos pudieran tratarse de fallecidos por COVID, vamos a aplicar el modelo que ya hemos visto con cifras oficiales de contagiados y fallecidos COVID, pero reemplazando los fallecidos oficiales COVID por el exceso de mortalidad por todas las causas observado con respecto a los valores esperados estimados del sistema MOMO. En este caso vamos a agregar los valores por edades en tres rangos de edad, menores de 65 años, entre 65 y 74 años y mayores de 74. La distribución de contagiados en esas franjas se hace usando la pirámide poblacional española por edades procedente del INE.
Modelo para mayores de 74 años
El resultado se muestra en la siguiente figura, en la que podemos observar cómo los excesos de fallecidos pueden tomar tanto valores positivos como negativos. Nótese que hemos reemplazado los puntos azules antiguos que se correspondían con fallecidos oficiales COVID por los excesos de fallecidos del MOMO con respecto al valor esperado. Pintamos además una media móvil a 21 días con una línea negra discontinua para detectar dónde está aproximadamente la media de los datos. La línea azul continua se corresponde con el modelo procedente de la aplicación del desfase de 1,96 días y una tasa de mortalidad de aproximadamente el 12,35%. Nótese que antes del 15 de febrero, aproximadamente, los datos reales de excesos de fallecidos (línea negra discontinua) están muy cercanos a los valores proporcionados por el modelo en función de los contagiados (línea continua azul), sin embargo, a partir del 15 de febrero se van por debajo hasta el 26 de junio, y a partir de ese momento están incluso por encima. Es decir, que si los excesos de fallecidos estuvieran vinculados a fallecimientos COVID esto indicaría que la vacuna no está teniendo efecto positivo ninguno en el porcentaje de gente que fallece con respecto a los contagiados.
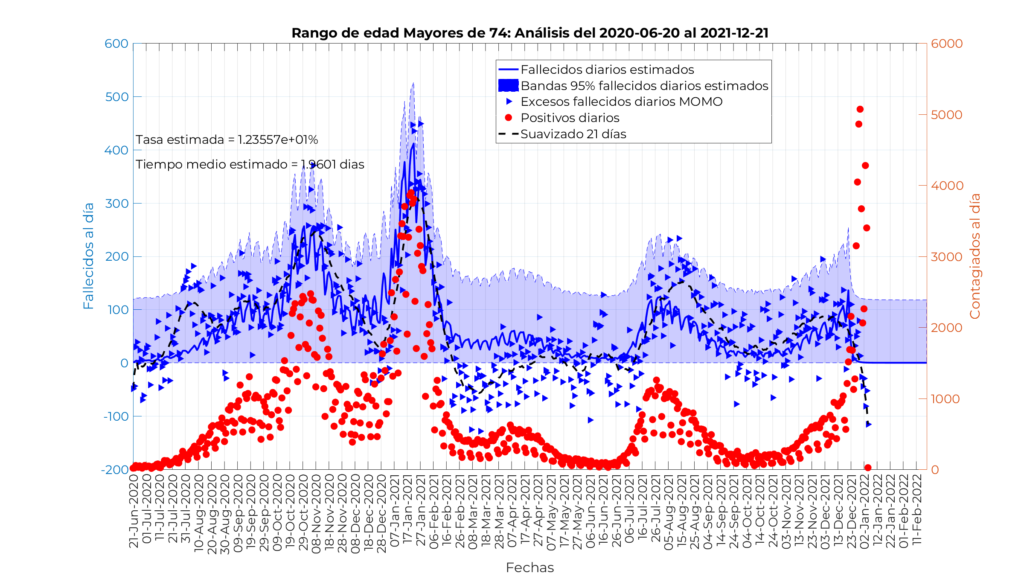
¿Qué está ocurriendo si la gente no se muere de COVID? Colegas con los que hemos compartido esta información nos dicen que el MOMO no funciona correctamente porque emplean una pirámide desfasada, aunque la metodología que emplea el MOMO a juzgar por las explicaciones que dan en la página oficial no parece contemplar la pirámide de población de forma explícita, y además los datos de 2019 están tan bien recogidos por las bandas de confianza que no nos convence ese argumento. Obviamente podemos poner en dudas todos los datos y métodos, la cuestión es que normalmente las explicaciones más sencillas son las más plausibles.
Si fuéramos conspiranoicos, podríamos dar dos posibles explicaciones:
- No se están contabilizando correctamente los fallecidos COVID.
- Está muriendo más gente de lo normal pero no por COVID, sino por los efectos secundarios de las vacunas. Ya sean directos o indirectos por el déficit de atención médica que se está dispensando a pacientes con otras patologías graves.
Obviamente esto no lo podemos constatar, pero tampoco entendemos que se dé por supuesto que algo funciona cuando hay motivos objetivos para dudar. A nosotros este resultado nos da que pensar y creemos que estamos siendo todos demasiado poco beligerantes con las farmacéuticas, teniendo en cuenta los pingües beneficios que están obteniendo.
¿Se repite este patrón para el resto de edades? Veámoslo.
Modelo para personas entre 65 y 74 años
En este caso el resultado si comparamos la media móvil a 21 días de los datos reales de excesos de fallecidos (línea negra discontinua) con respecto a los valores proporcionados por el modelo en función de los contagiados (línea continua azul) están muy cercanos. El modelo reproduce el comportamiento de los fallecidos correctamente como un porcentaje de los contagiados de aproximadamente el 2.6 % y con un desfase de unos 15,5 días. Es decir, en esta franja de edad la vacuna parece no haber tenido influencia ninguna en los excesos de mortalidad. El resultado es análogo al anterior.
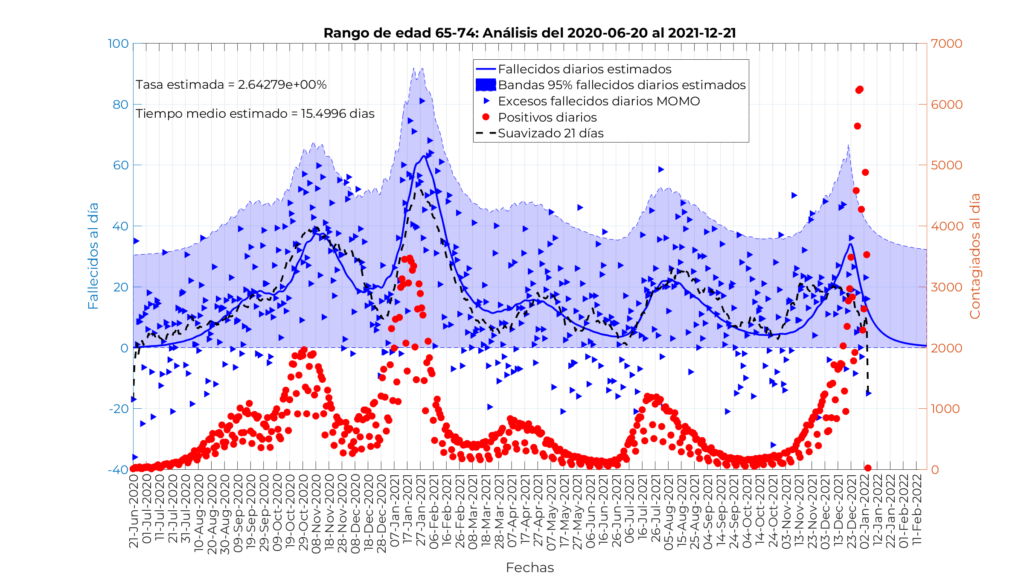
Modelo para personas menores de 65 años
En este caso el resultado si comparamos la media móvil a 21 días de los datos reales de excesos de fallecidos (línea negra discontinua) con respecto a los valores proporcionados por el modelo en función de los contagiados (línea continua azul) están también muy cercanos. El modelo reproduce el comportamiento de los fallecidos correctamente como un porcentaje de los contagiados de aproximadamente el 0.082 % y con un desfase de unos 13,7 días. Análogamente a los casos anteriores, en esta franja de edad la vacuna parece no haber tenido influencia ninguna en los excesos de mortalidad.
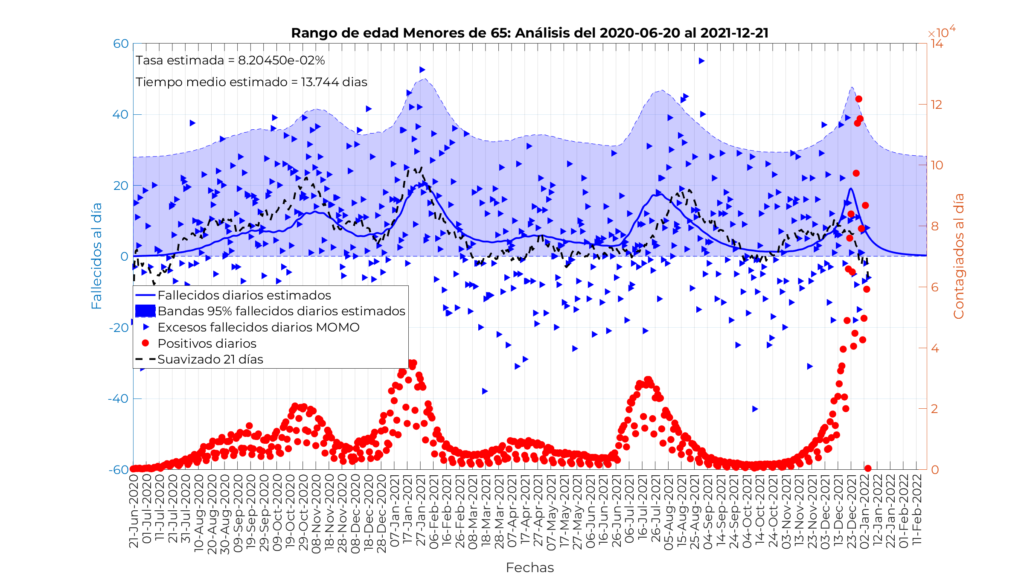
2
Conclusiones
Como podemos observar, en función de los datos oficiales que se empleen hay razones fundadas para dudar de la efectividad real de las vacunas como reductoras de la mortalidad en función de los contagiados. No entendemos que estemos dando por supuesto hechos que como hemos demostrado en este análisis pueden ser el resultado de un análisis inapropiado, como por ejemplo, la no discriminación por edades.
Sirva este artículo para llamar la atención sobre la efectividad real de las vacunas. En entornos con incertidumbre no es buena estrategia poner todos los huevos en la misma cesta, que es lo que hacen nuestros gobernantes al confiar todas sus esperanzas en la vacunación global. Y por favor, respetemos a los no vacunados porque tiene motivos justificados para no vacunarse.
Material adicional
Como complemento adicional a este artículo os recomendamos escuchar el siguiente Pod Cast sobre la vacunación. Suscribimos al 100% todo lo que en él se comenta.